*Bernardo Estellita Lins
Um recente artigo do economista Bernardo Mueller, professor da Universidade de Brasília, chama a atenção para os riscos de enfrentarmos comportamentos caóticos em políticas públicas. Em geral, quando ouvimos a palavra “caos” tendemos a pensar em um comportamento desorganizado, fora de controle, talvez devido a falhas ou erros atribuíveis a autoridades ou responsáveis. Mas a realidade é mais complicada e merece ser melhor examinada.
Para explicar a racionalidade por trás do caos, dois sociólogos norte-americanos, Douglas Kiel e Euel Elliott, propuseram nos anos noventa um exercício simples, que podemos reproduzir em uma planilha sem grandes dificuldades. Trata-se de um exercício matemático. Suponha que o comportamento de uma variável ao longo do tempo sofra a influência de seu passado. E suponha que esse vínculo não seja linear. Se chamarmos essa variável de x, em cada período t teremos uma relação com o seu valor em t – 1, ou seja, no período imediatamente anterior.
Suponha que essa relação, e aqui me permito um pouco de matemática, seja algo como:
xt = k . xt – 1 . (1 – xt – 1)
Na expressão, k é um parâmetro que quantifica o efeito intertemporal, ou seja, o quanto que o valor da variável x no período anterior afeta seu comportamento no período atual.
Proponha um valor inicial para x. Para que o exemplo funcione, terá que ser um valor menor que 1. Monte sua planilha, construindo os valores de x para cada período, com t igual a 1, 2, 3 e assim por diante. A seguir, construa um gráfico mostrando o comportamento da variável, período a período.
Tive a paciência de montar esse exercício, fazendo uso de diversos valores para o multiplicador k. E gerei os gráficos correspondentes. Dependendo de variações no formato da expressão acima, o resultado do seu exercício, se você, caro leitor, quiser experimentar seu adestramento no Excel, poderá diferir um pouco. Mas eu cheguei ao resultado que descrevo a seguir. Em todos os casos usei um valor inicial de x1 = 0,95.
Com um valor pequeno de k, o gráfico resultante é bem-comportado. Para k = 0,8, por exemplo, teremos algo como o desenho a seguir:
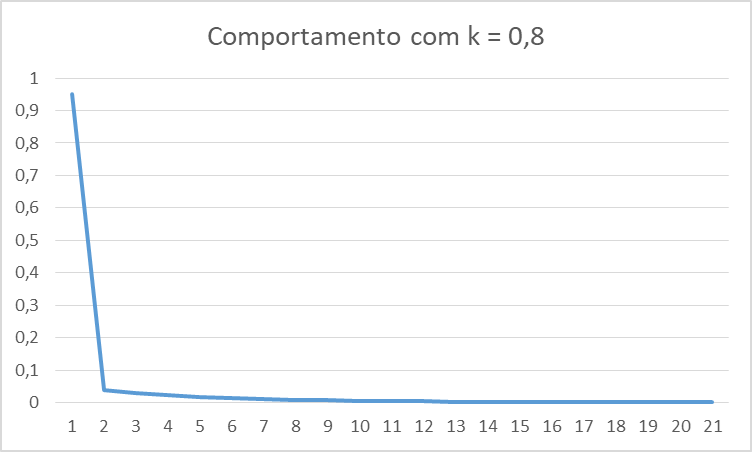
A influência do período precedente rapidamente se desfaz, a variável tende a zero. O valor inicial, o “choque” de x1 = 0,95 não resultou em efeito relevante após o oitavo ou nono período. Dizemos que x* = 0 é o estado estacionário ao qual o modelo converge.
Porém, se escolhermos um valor maior para k, a influência do passado torna-se permanente. Por exemplo, com k = 2,2 haverá um resíduo permanente:
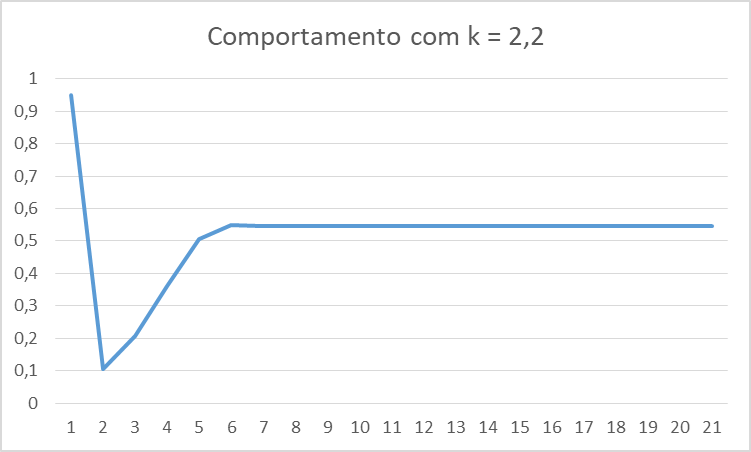
Vejam, não houve outras variáveis, outros fatores em jogo. Apenas o já conhecido valor inicial de x1 = 0.95, que se perpetuou ao longo do tempo e tornou-se um efeito permanente. O interessante desse comportamento é que, no primeiro período após o “choque”, há uma queda acentuada do valor, para em seguida este se recuperar. O que fizemos? Nada. É apenas a influência do passado que se torna persistente. O estado estacionário será dado por x* = 0,545.
Finalmente, vamos considerar um valor elevado, de k = 3,8. O efeito intertemporal é significativo. O gráfico muda de comportamento:
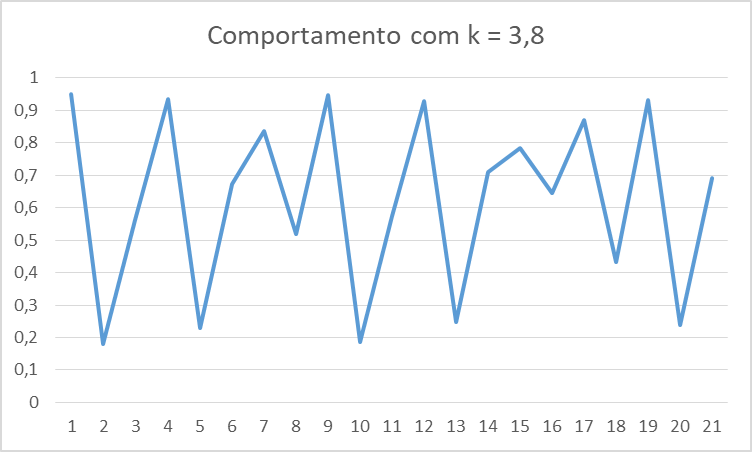
O valor de x se alterna entre elevações e quedas abruptas. O “choque” torna o processo caótico. Essa aparente desordem, no entanto, tem uma descrição matemática precisa, dada pela nossa equação inicial, com a escolha de um fator de influência alto. Não houve, ao longo do tempo, qualquer outra intervenção. A conexão intertemporal é aquilo o que leva a esse comportamento. Não existe um estado estacionário, não existe nem sequer um ciclo estável que possa ser reconhecido ou uma regularidade estatística simples.
Nesse comportamento, os limites entre os quais a variação se estabelece (algo como uma quota superior de 0,94 e uma quota inferior de 0,18) formam uma bacia dentro da qual os valores da variável se situam.
O exercício que mostramos é uma conversa de engenheiro para engenheiro. Tem limitações e seu objetivo é meramente didático. No mundo real, porém, muitas das atividades produtivas que acompanhamos e muitos dos processos sociais que vivemos exibem aspectos desse comportamento. Pensem, por exemplo, na pandemia COVID-19. A introdução de um agente patogênico em um pequeno número de contaminados ao final de 2019, o “choque” inicial, criou uma onda de contaminação e de mortes que se estendeu por dois anos, com altos e baixos. As estratégias de controle ensaiadas nesse período tiveram efeito temporário. Quando retiradas, a epidemia voltava, com seu comportamento assustador.
O procedimento correto, nesses casos, é identificar o canal pelo qual ocorre o vínculo entre um período e outro. Na COVID-19, esse vínculo era dado pelo contágio e a incubação do vírus em outra pessoa. Medidas de higiene, por exemplo, cortam o contágio, a vacina corta a incubação e subsequente contaminação.
Há outros mecanismos e canais pelos quais um comportamento caótico se instala em um processo. Bernardo Mueller relaciona alguns deles, que ocorrem em sistemas complexos: o comportamento evolutivo do sistema, a reatividade dos agentes envolvidos, a presença de fatores desconhecidos ou difíceis de identificar, o número grande de relações que se estabelecem nesses sistemas.
Em processos que podem reverter a um comportamento caótico, nossa abordagem usual de buscar, período a período, uma relação de causalidade entre as grandezas que consideramos relevantes pode estar fadada ao fracasso. Há outros canais que precisamos identificar, para que possamos compreender o que está ocorrendo e que estão além da visão e dos métodos convencionais de análise. Mais do que sugerir uma abordagem de trabalho, o propósito deste breve artigo foi o de mostrar, com um exemplo palpável, como esse comportamento pode se instalar em um modelo simples. E alertar para que sejamos sempre humildes. Sistemas complexos escondem armadilhas desse tipo e compreendê-los é uma tarefa intelectual desafiadora, que pode jogar por terra pressupostos que damos por garantidos.
Para quem quiser se aprofundar:
MUELLER, Bernardo P. Why public policies fail: Policymaking under complexity. Economia, 21 (2020) 311–323.
KIEL, Douglas e Euel ELLIOTT. Exploring nonlinear dynamics with a spreadsheet: a graphical view of chaos for beginners. In: Chaos Theory in the Social Sciences. Ann Arbor: Unoversity of Michigan Press, 1997, pp. 19-29.
Bernardo Estellita Lins é Acadêmico da ABQ. Engenheiro Civil pela UnB – Universidade de Brasília. Mestre e Doutor em Economia. Tem especialização em Análise de Sistemas pela UCB. Examinador e Examinador Sênior do PNQ e do Prêmio da Qualidade do Governo Federal. E tem mais de 20 artigos publicados ou apresentados em eventos sobre Qualidade.







